자율 주행 자동차의 스티어링 제어 방법 : Vehicle Lateral Control

2021.09.03 - [Autonomous Navigation/Control] - 자율 주행 시스템 : 행동(Action) 단계

자율 주행 시스템 : 행동(Action) 단계

지난 글에서 알아보았듯, 인지-계획 단계를 거쳐 이동해야 할 경로가 주어졌다면 그 경로를 추종하기 위해 스티어링과 엑셀, 브레이크를 어떻게 조작해야 할지 계산해야 합니다. 가장 복잡한 부분은 스티어링 모델로, 이 글에서는 임의의 경로를 추종할 수 있는 3가지의 스티어링 제어 방법에 대해 알아보겠습니다.

 

* 그림은 https://dingyan89.medium.com/three-methods-of-vehicle-lateral-control-pure-pursuit-stanley-and-mpc-db8cc1d32081를 참조하였습니다.

 

0. Cross-track error

 

일단 스티어링 제어 방법의 성능 지표 중 하나인 cross-track error에 대해 알아보겠습니다.

 

Cross-track error는 위 그림에서의 $ e $에 해당합니다. 복잡하지 않습니다. 현재 차량의 이동 방향 벡터(를 연장한 직선)와 목표점 사이의 횡방향 거리를 뜻합니다.

 

1. Pure pursuit controller

 

Pure pursuit 알고리즘은 경로상의 한 점인 look-ahead point와 reference point인 차량의 후륜 중앙 사이의 위치 관계를 이용해 스티어링 조작을 명령합니다. 

 

Pure pursuit controller에서 사용하는 변수

이 상태에서의 목표는 trajectory로 이동하는 것입니다. $ L $은 전후륜간의 거리, $ \alpha $는 차량의 heading과 (look-ahead point와 reference point를 잇는 직선)사이의 각도, R은 turning radius입니다. 변수들 사이의 관계는 다음과 같습니다.

 

 

Bicycle model을 사용한다면 조향각 $ \delta = arctan(\frac{L}{R}) = arctan(\frac{2L\cdot sin(\alpha)}{l_{d}}) $로 나타낼 수 있습니다. Problem formulation에서 알 수 있듯, 차량에 작용하는 힘들은 모두 무시하고 기하학적인 관계만을 사용해서 조향각을 산출합니다. 또 조향각 산출식에서 알 수 있듯 look-ahead distance가 작으면 조향각이 커지게 되고, 조향각이 크면 고속에서는 대참사가 벌어질 수 있습니다. 따라서 보통 look-ahead distance는 속도에 비례해 길게 잡습니다(파라미터 x 속력 정도로 계산하면 되겠습니다).

 

Pure pursuit controller에서 cross-track error $ e = l_{d}\cdot sin(\alpha) $ 이므로 위의 식 중 곡률 $ k $를 구하는 식과 연립해 보면 $ k = \frac{2}{(l_{d})^{2}}e $ 입니다. 즉 cross-track error가 클수록 큰 곡률로 회전해 경로를 추종합니다. Look-ahead distance의 섬세한 튜닝이 필요함을 다시 알 수 있습니다.

 

 

2. Stanley controller

 

Stanley controller는 pure pursuit controller와는 달리 차량 전륜의 중앙을 reference point로 잡고, heading error와 cross-track error를 모두 고려합니다. 이 방식에서의 변수들은 다음과 같습니다.

 

Heading error $ \Psi $는 trajectory heading과 vehicle heading 사이의 각도이고, cross-track error는 이전과 유사합니다. 여기에서의 목표는 steering angle $ \delta $를 $ \Psi $와 같게 만드는 것, 그리고 cross-track error를 0으로 만드는 것입니다. Steering angle은 다음과 같이 주어집니다.

 

$ \delta (t) = \psi (t) + tan^{-1}\left ( \frac{ke(t))}{k_{s}+v_{f}(t)} \right )$

$ \delta (t) \epsilon [\delta_{min}, \delta_{max}] $

 

$ \delta_{min} $ 과 $ \delta_{max} $는 최대 조향각, $ k_{s} $는 분모가 0이 되도록 하지 않는 constant입니다. Stanley controller가 pure pursuit controller 보다 더 우수한 점은 track으로의 자연스러운 접근이 가능하다는 점입니다. 이것이 어떤 느낌인지는 Stanley controller에 의해 생성되는 경로를 살펴보면 알 수 있습니다.

 

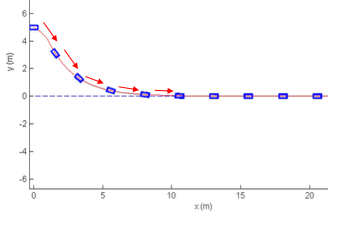
즉, 비교적 큰 heading error와 cross track error를 모두 핸들링할 수 있습니다.

 

 

3. Model Predictive Controller

 

Model Predictive Controller(MPC)는 위의 두 방식과는 다르게 cost function을 최소화하는 방식의 controller입니다. 또한 이상적이고 기하학적인 formulation을 사용하지 않고 차량(system)의 모델을 제어에 반영합니다.