그래프 기반 SLAM의 동작 방식

이 글에서는 그래프 기반 SLAM의 전반적인 작동 방식을 설명합니다. 수식이 포함된 보다 디테일하고 엄밀한 설명은 코드 리뷰와 함께 진행할 예정입니다.

 

다음과 같은 자료를 참조하였습니다.

1. https://www.youtube.com/watch?v=saVZtgPyyJQ (MATLAB YouTube 채널 - Understanding SLAM Using Pose Graph Optimization)
2. https://www.ipb.uni-bonn.de/msr2-2020/ (Cyrill Stachniss 교수님의 Mobile Sensing and Robotics 강의자료)

먼저 여기에서 말하는 그래프가 무엇인지 알고 가 보기로 합시다. 일반적으로 그래프는 Node(Vertex)와 Edge로 구성된 자료 구조를 말합니다. 

 

그래프 자료구조의 모습

 

Node와 Edge에 각각 뭐가 들어가야 한다~ 고 정해져 있는 것은 아닙니다. 이런 식으로 데이터를 표현하면 편할 때에 그래프를 사용하면 될 뿐, Edge는 반드시 Node사이의 어떤 것을 설명해야 한다거나 그런 조건은 없습니다.

 

그래프 기반 SLAM에서는 로봇의 Pose를 그래프의 Node로 표현하고 그 Pose 사이의 구속조건을 Edge로 표현합니다. 2D SLAM을 예로 들어 설명해 보겠습니다. $ t $ 번째 Pose가 $ (1.5m, 2.2m, 65^{\circ}) $ 라고 하고, 측정된 이동량이 $ (0.7m, -0.3m, 17^{\circ}) $ 라고 하면, $ t+1 $ 번째 Pose의 추정값은 $ (2.2m, 1.9m, 82^{\circ}) $라고 할 수 있을 것입니다. 그러면 $ t $번째와 $ t+1 $ 번째 Pose가 각각 $ t $번째와 $ t+1 $번째 Node가 되고, 그 사이에 측정된 이동량이 두 Node 사이의 Edge가 됩니다.

 

(보통은 로봇의 최초 위치를 원점으로 놓고, 이동량 측정은 다양한 센서를 사용합니다. 바퀴의 회전 횟수를 세어서 이동량을 구하는 wheel odometry를 사용할 수도 있고, 카메라를 이용한 visual odometry를 사용할 수도 있습니다. Visual odometry에 대해서는 추후 설명하도록 하겠습니다)

 

이렇게 매 step마다 Node와 Edge를 추가해 나가면 마지막에는 길게 연결된 그래프가 만들어지게 됩니다. 여기에서 두 가지 의문이 들면 됩니다.

 

1. 측정에는 반드시 오차가 포함된다고 했는데, 저렇게 그냥 측정값을 믿고 다음 Pose를 계산해도 되는 건가?
2. 그래서 이 그래프를 가지고 어떻게 오차를 보정한다는 걸까? 그냥 데이터를 쭉 써놓은 것 같은데...

그렇습니다. 이대로 두면 오차도 보정되지 않았고, 그림으로 그렸다는 것 외에 별 의미도 없는 그래프가 만들어졌을 뿐입니다. 하지만 그래프 기반 SLAM에는 오차를 보정하기 위한 중요한 개념이 포함되어 있습니다.

 

바로 연속적이지 않은 Node사이에도 Edge가 존재할 수 있다는 것입니다.

 

이게 무슨 말이고, 오차 보정에 어떤 도움이 되는 것일까요? 1번 참조자료를 사용하며 설명해 보겠습니다.

 

 

일단 이전 글에서 언급한 것처럼 위치 추정에 오차가 있어(wheel odometry 센서가 싼마이라던지, 바퀴가 미끄러졌다던지 하는 상황을 생각해볼 수 있습니다. 그리고 그런 상황이 아니더라도 센서에는 반드시 오차가 존재합니다) 잘못된 지도가 작성된 상황입니다. 그리고 로봇의 위치/방향(Pose)을 Node, 매 step마다 측정된 이동 거리와 방향(odometry)을 Edge로 하는 그래프가 그려져 있습니다. 이제 다시 한번 떠올려 봅시다. 이동 거리와 방향 측정이 불안정하기 때문에, 그리고 오차는 누적되기 때문에 Pose는 뒤로 갈수록 점점 믿을 수 없게 됩니다. 즉 지금 그래프의 Pose는 확정된 것이 아니고, 나중에 보정 절차가 들어가야 합니다. Odometry도 마찬가지입니다.

 

이제 이해를 돕기 위해, 저 그래프의 Edge(붉은색 선)을 늘어났다 줄어들었다 할 수 있는 용수철로 생각해 봅시다. 지금 저 상태에서는 (오차가 있는) 용수철들을 순서대로 이어 붙여놓은 것뿐이므로, 오차를 보정할 방법도 없고 그래프는 안정된 상태(용수철이 늘어나거나 줄어들지 않은 상태)입니다. 하지만 용수철들은 추가적인 구속 조건이 있다면(오차를 보정할 방법이 있다면) 길이가 변할 수(오차가 보정될 수) 있습니다. 다음과 같은 상황을 한 번 보겠습니다.

 

 

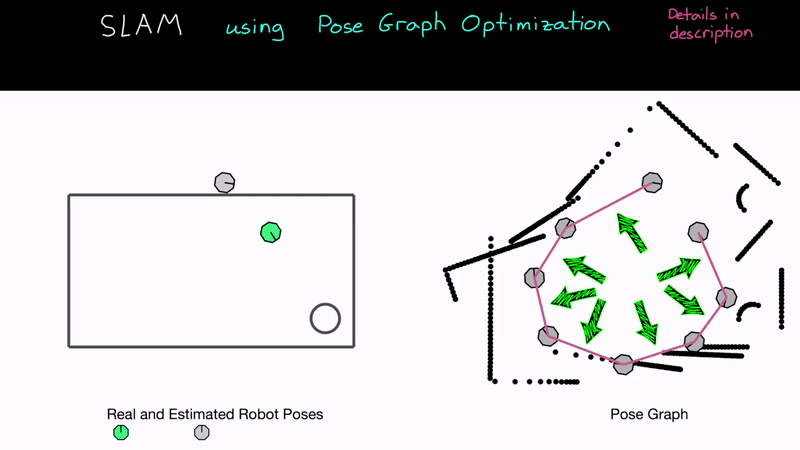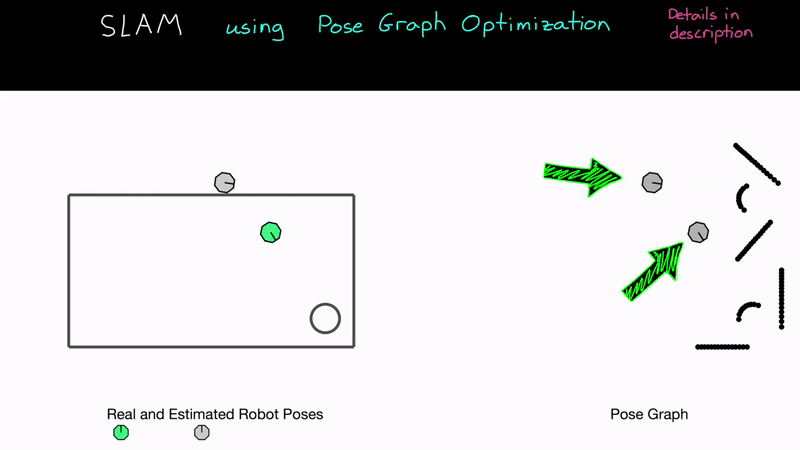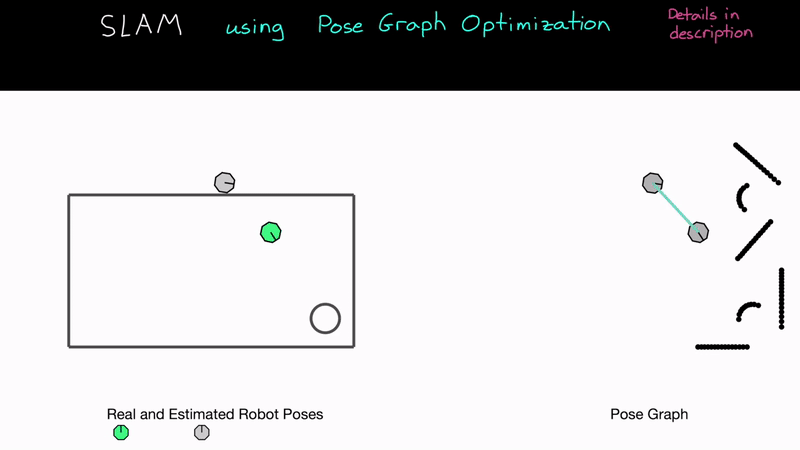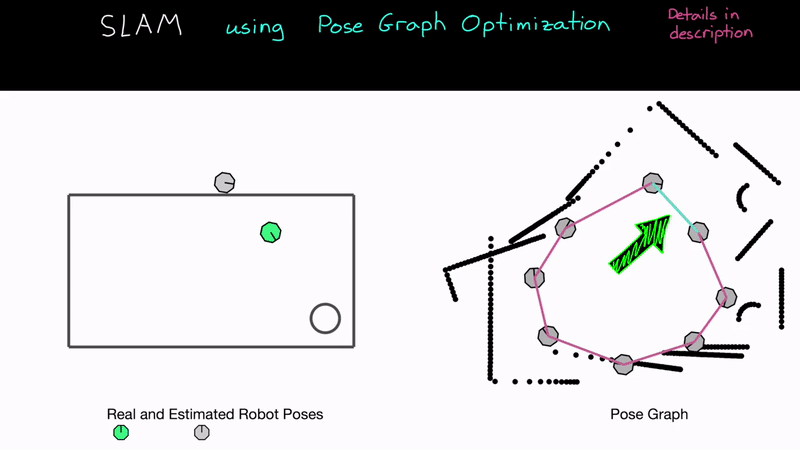
로봇이 대강 한 바퀴를 돌아 처음 비스무리한 위치로 돌아왔더니, 얼마 전에 어떤 위치에서 관측했던 LiDAR 데이터와 똑같은 모양의 데이터가 관측된 것입니다!! 즉 이를 통해 현재 위치가 그 '어떤 위치' 주변이라는 것을 추정할 수 있습니다. 이건 엄청 중요한 일입니다. 오차가 누적됨에 따라 현재 위치를 믿을 수 없게 되었는데, 이제는 현재 위치가 대략 어디 주변인지에 대한 정보를 얻었기 때문에 불확실성이 크게 줄어들게 된 것입니다.

 

이에 따라 그 '얼마 전의 위치'와 '현재 위치' 사이에 Edge를 추가할 수 있게 됩니다. 일단 현재의 LiDAR 데이터를 어떻게 이동해야(=거리, 방향) 얼마 전의 LiDAR 데이터와 잘 포개지는지(일치하는지) 알아봅니다. 이를 계산하는 방법을 ICP(Iterative Closest Point)라고 하는데, 주로 LiDAR 데이터 (Point Cloud)끼리 정렬하는 데 쓰이는 방법입니다. ICP에 대해서도 나중에 시간이 있으면 설명해 보도록 하겠습니다. 센서의 종류에 따라 이전 데이터와 현재 데이터를 연관시켜서 Edge(두 위치 사이의 관계, 즉 거리와 방향)를 만드는 방법은 다양한데, 예를 들어 스테레오 카메라 기반 SLAM에서는 2차원 영상의 기하학적 특성을 사용해 두 데이터 사이의 거리와 방향을 알아냅니다(이론 설명 및 코드 리뷰 때 자세히 설명하도록 하겠습니다).

 

어떻게 이동해야 두 데이터가 잘 포개지는지 알아냈다면, 반 이상 성공한 것입니다. 이게 바로 '얼마 전의 위치'에 해당하는 Node와 '현재 위치'에 해당하는 Node 사이의 Edge입니다. Edge는 구속 조건, 관계 등으로 생각할 수도 있겠습니다. 여기까지가 위에서 언급한 연속적이지 않은 Node 사이에 Edge가 생기는 과정입니다. 그럼 다음으로 넘어가 보겠습니다.

 

 

이제 꽤 볼만한 일을 할 수 있습니다. 이 연속적이지 않은 Node 사이의 구속조건을 사용해서(위 영상의 경우에는 이전 위치와 현재 위치가 일치한다는 것이 구속조건입니다. 굳이 일치하는 게 아니더라도 정확한 위치 관계만 있으면 됩니다) 그 구속조건에 맞도록 그래프를 찌그러뜨리는(Edge와 Node들을 변형시키는) 작업을 하면 됩니다. 현재까지의 부정확한(크게 믿을 수 없는) Pose들에 비해 새로운 구속조건은 꽤 정확(강력)하다고 할 수 있기 때문에, 로봇의 이동 경로(그래프)가 물리적으로 좀더 "말이 되려면" Edge와 Node 들이 이 강력한 구속조건이 성립하도록 변형되고 이동되어야 하는 것입니다! 이 과정을 그래프 최적화(Graph Optimization)이라고 합니다.

 

이 과정을 수행하고 나면 위의 영상에서 볼 수 있듯, 잘못 만들어진 지도와 경로 데이터가 꽤 정확하게 보정된 것을 볼 수 있습니다. 아직 완벽하지는 않습니다. 정확도를 더 개선하려면 BA(Bundle Adjustment)를 지속적으로 수행하거나, 더 많은 구속조건을 추가하거나 등의 절차가 필요합니다. Bundle Adjustment도 아주 중요한 작업이기 때문에 이것도 이론 설명 및 코드 리뷰 때 자세히 설명하도록 하겠습니다.

 

이렇게 이전에 방문했던 장소로 다시 돌아왔다는 사실을 인식하고, 그 위치와 현재 위치 사이의 정확한 관계(거리, 방향)을 알아내고, 이걸 그래프에 Edge로 추가하고, 그래프 최적화를 수행하는 과정까지를 루프 폐쇄(Loop Closure)라고 부릅니다. 루프 폐쇄는 그래프 기반 SLAM의 가장 중요한 요소이며, 그래프 기반 SLAM이 개발된 이유 자체가 루프 폐쇄를 적극적으로 활용하기 위해서라고 해도 좋을 정도입니다. 그렇기 때문에 정확한 루프 폐쇄는 매우 중요합니다. 특히 치명적인 것은 이전에 방문했던 장소가 아닌데도 방문했던 장소로 오인식하는 경우이며, 이 경우에는 틀린 구속조건이 생성되기 때문에 이대로 그래프 최적화를 수행하면 아래와 같은 대참사가 일어납니다.

 

 

즉 멀쩡하던 그래프와 지도가 틀린 모양으로 찌그러지게 됩니다. 심각한 문제이기 때문에, 루프 폐쇄 알고리즘들은 오인식 문제가 일어나지 않도록 하기 위해 몇 중의 검사를 통과해야 Loop로 인정하는 절차를 포함하고 있습니다. 이것 또한 이론 설명 및 코드 리뷰 때 설명할 계획입니다.

 

지금까지 그래프 기반 SLAM과 루프 폐쇄에 대해 최대한 직관적으로 설명하려고 노력했지만, 이 개념을 코드로 옮기려면 수학적으로 정의되어야 할 부분이 많습니다. 일단 비슷한 데이터가 맞는지 인식할 수학적 방법도 필요하고, 두 데이터 사이의 이동 거리와 방향을 정확하게 계한할 알고리즘도 필요하며, 그래프를 어떻게 정확하게 찌그러뜨릴지(최적화 수행)에 관한 방법론도 필요합니다. 이를 위해 행렬과 선형대수, 최적화 기법 등에 대한 전반적인 이해가 필요합니다. 스테레오 카메라 기반 SLAM의 경우에는 영상 기하학과 특징 추출에 대한 이해도 필요합니다. 최근에는 비슷한 장소가 맞는지 영상 기반으로 인식하기 위해 심층학습을 사용하는 경우도 꽤 있다고 합니다.

 

수학적인 정의와 해법에 대해서는 이론 설명 및 코드 리뷰 때 함께 설명할 계획입니다. 그래도 정확한 이해를 위해서는 미리 공부를 해놓거나, 아니면 코드 리뷰 때 등장하는 몇 가지 키워드(Projective n Points, Levenberg-Marquardt)등을 이용해 검색하며 필요한 부분을 알아두는 것이 좋겠습니다. 미리 공부를 하고 싶으시다면 이런 블로그들을 방문해 보시는 것을 추천드립니다.

 

이제 더 구체적인 수학적 원리와 논리 흐름을 알고 싶으시다면, 이론 설명 및 코드 리뷰 카테고리의 글들을 읽으시면 됩니다.